課題0: 復習

(出題4月15日，締切5月13日)

Last modified: Wed Apr 9 2025

このページは，基礎工学部システム科学科機械科学コース2年生向けの「情報科学演習」における課題0について説明するページです．

この課題の目的は，5月13日までに

昨年の復習．
エディタの使い方，プログラムの作り方の確認．
この授業の事前知識の確認．

を行なうことである．また，この課題を通じて，この授業における課題の処理手順をよく理解してもらいたい．

この授業は，この課題程度のプログラムが作成できる受講生を対象にしている．

プログラムの作成がままならぬ人は，かなり焦る必要がある．連休を返上して，勉強すること．自分で調べたり，考えたりしてもわからない場合は，そのままにせずに，必ず担当のTAに相談すること．

課題0-0～0-8のうちできるだけ多くの項目に取り組む．その中で自分が一番苦労したと思うもの，あるいは，一番力作だとものを一つ選び提出する．

提出物は以下の通り．

プログラムリストを提出用プログラムの書き方のページの指示に従った形式で整えたもの．
プログラムの動作がよく確認できる実行例をいくつか．

内容ができていても形式が不適切な場合は合格にしないので，注意すること．

課題を解くにあたっての一般的注意

課題の文中で特に指定していないものでも，処理の中心部分はできるだけ関数化してみよう
1度のプログラムの実行で，繰り返し処理ができるようにしてみよう．

例

#include <stdio.h>

/* プロトタイプ宣言 */
int f(int i);

int
main(void)
{
    int x, y;

    while ( 1 ) { /* 簡単のため無限ループにしている．*/
        printf("x = ");
        scanf("%d", &x);
        y = f(x);
        printf("y = %d\n", y);
    }

    return 0;
}

/* 引数の2乗を計算する関数 */
int
f(int i)
{
    return i*i;
}

■課題0-0: 汎用九九表

【ポイント】条件分岐，二重ループ，出力書式

整数rmin, rmax, cmin, cmaxを入力すると，行がrmin～rmax, 列がcmin～cmax の九九の表を作成せよ．値が負の場合や，rmin>rmaxや， cmin>cmaxの場合にも対応できるようにせよ．どのように対応するかは各人で考えよ．例えば，

    rmin? 7
    rmax? 5
    cmin? -3
    cmax? -1

      |  -3  -2  -1
    --+-------------
     7| -21 -14  -7
     6| -18 -12  -6
     5| -15 -10  -5

rmin, rmax, cmin, cmaxの全てに0が入力されたら，プログラムを終了する．

■課題0-1: 級数

【ポイント】繰り返し，整数どうしの割り算

整数nを入力し，以下の級数

(1/1+1/4+1/9+…+1/n²)を計算して結果を表示せよ．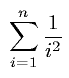

■課題0-2: 最大値

【ポイント】繰り返し，条件分岐

最初に整数nを入力し，その後，「i番目の数値を入力して下さい」(1≦i≦n) と表示しながらn個の実数を読み込む．入力された実数値の中で，もっとも大きなものが何番目だったかとその値を出力せよ．同じ値が複数あった場合は，一番後に入力されたものの番目を表示する． n≦0の場合はプログラムを終了する．

■課題0-3: 複利計算

【ポイント】繰り返し，整数どうしの割り算

毎月a円貯金し，1ヶ月貯金するとb%の利子が付く．つまり，1ヶ月後には， a(1+b/100)円，2ヶ月後には(a(1+b/100)+a)(1+b/100)円，… 同じように繰り返していって，1000000円を越えるのは何ヶ月か求めよ． a≦0の場合はプログラムを終了する．aは整数，bは実数とする．

■課題0-4: 平行ベクトル

【ポイント】ゼロ除算，浮動小数点数の扱い

実数値a,b,c,dを入力する． 2つの2次元ベクトル(a,b)と(c,d)が平行かどうかを調べてその結果を表示せよ．処理の中で，0による除算や浮動小数点数の等値演算(==)をしないように考慮せよ．

(0.1, 0.3)と(1.0, 3.0)の判定ができるか?
(1.0, 0.0)と(2.0, 0.0)の判定ができるか?
(0.0, 1.0)と(0.0, 2.0)の判定ができるか?
(0.0, 0.0)と(1.0, 0.0)の判定ができるか?

■課題0-5: 四捨五入

【ポイント】浮動小数点数の扱い，関数

double型を引数に取り，その小数部を四捨五入した値をint型で返す関数を作り，その動作を確認するプログラムを作る．負の値にも対応すること．標準ライブラリ関数を使うものと，使わないものの2種類を作ってみよう．

■課題0-6: 場合分け

【ポイント】条件分岐，関数

数学的には以下のように表現される関数をCの関数 (引数double型，戻り値double型)として作成し，その動作を確認するプログラムを作る．

■課題0-7: 整数乗関数

【ポイント】条件分岐，繰り返し，関数

double型の引数xとint型の引数yをとり，xのy乗をdouble型として返す関数を作成し，その動作を確認するプログラムを作る．yが0以下の場合にも対応すること．標準ライブラリ関数のpow()を使わずに，整数乗に特化した関数を作る．

■課題0-8: 回転変換

【ポイント】無駄な計算をしない，二重ループ，出力書式

実数tを入力する．2次元座標(x,y)を原点回りにt度回転させて(x', y') へ移動させる以下のような変換を考える．

    x' = cosθ・x - sinθ・y
    y' = sinθ・x + cosθ・y

ただし，この式はC言語の表現とは異なることに注意．また，θはtをラジアン単位で表現したものとする．この変換によって，2次元座標の集合(x,y) (x=0,1,…, 10, y=0,1,…,10, 11×11の格子点) のそれぞれの点がどこへ移動するか計算し，その結果を以下のように桁をそろえて綺麗に表示せよ．

(  0.000000,   0.000000)  →  (  0.000000,   0.000000)
(  0.000000,   1.000000)  →  (  X.XXXXXX,   X.XXXXXX)
(  0.000000,   2.000000)  →  (  X.XXXXXX,   X.XXXXXX)
       :           :                 :           :
( 10.000000,  10.000000)  →  (  X.XXXXXX,   X.XXXXXX)